5. Určení velikosti ložiska
Najít distributora
5.1 Všeobecné informace
Správně namontované a mazané valivé ložisko bude v provozu za normálních podmínek, tj. bez extrémních rychlostí a teplot, vyřazeno únavou materiálu na funkčních plochách. Opakované namáhání na stykových plochách mezi valivými tělesy a kroužky se projeví po určité době podle velikosti zatížení jako únavová trhlinka. Ta se rozšiřuje, až se vyštípne část materiálu kroužku ložiska nebo valivého tělesa (pitting) a způsobí poruchu. Mnohá ložiska se vyřazují z činnosti i pro jiné důvody než je únava materiálu, ale těmto poruchám se lze vyhnout, je-li s ložiskem správně zacházeno, je-li ložisko správně namontováno a mazáno a není-li přetěžováno.Zkouší-li se určitý počet stejných ložisek na únavu při stanovených provozních podmínkách (zatížení a otáčky), vyskytuje se velký rozptyl trvanlivosti mezi jednotlivými ložisky. U skupiny 30 nebo více ložisek může být poměr mezi nejkratší a nejdelší trvanlivostí řádově 20 i více. Pro každou zkoušenou skupinu ložisek lze nakreslit křivku rozptylu trvanlivosti, znázorňující závislost mezi trvanlivostí a množstvím ložisek, která byla vyřazena.
Potřebná velikost ložiska se stanoví na základě působících vnějších sil a podle požadavků na trvanlivost a spolehlivost ložiska v uložení. Velikost, směr, smysl a charakter zatížení ložiska jakož i provozní frekvence otáček jsou rozhodující pro volbu druhu a velikosti ložiska. Přitom se musí také přihlížet na další zvláštní nebo důležité podmínky každého jednotlivého případu jako např. provozní teplotu, prostorové možnosti, jednoduchost montáže, požadavky na mazání, těsněni atd., které mohou ovlivnit výběr nejvhodnějšího ložiska. Pro dané konkrétní podmínky mohou v mnohých případech vyhovovat různé typy ložisek.
Z hlediska působení vnějších sil a funkce ložiska v příslušném uzlu nebo celku rozlišujeme v ložiskové technice dva typy zatížení valivého ložiska:
- Pokud se ložiskové kroužky navzájem relativně vůči sobě otáčejí a ložisko je za tohoto stavu vystaveno působení vnějších sil (což platí pro většinu případů použití ložisek), jde o dynamické zatížení ložiska,
- Pokud se ložiskové kroužky buď navzájem nepohybují, nebo se pohybují velmi pomalu, ložisko přenáší kývavý pohyb nebo vnější síly působí kratší čas, než je čas jedné otáčky ložiska, jde o statické zatížení ložiska.
5.2 Spolehlivost valivých ložisek
Spolehlivost skupiny zjevně stejných valivých ložisek pracujících za stejných podmínek je v procentech vyjádřená část skupiny, u které se očekává, že dosáhne nebo překročí stanovenou trvanlivost.Spolehlivost jednotlivého valivého ložiska je pravděpodobnost, že ložisko bude dosahovat nebo překračovat stanovenou trvanlivost.
Rovnice pro výpočet trvanlivosti zahrnuje vliv napětí vyvolaného vnějším zatížením, mazáním a kinematikou ploch v místě valivého styku. Zahrnutí vlivu komplexního systému napětí na trvanlivost ložiska umožňuje lépe předpovědět skutečné chování ložiska v konkrétním uložení. Mezinárodní normy, jako např. ISO 281, jsou založeny na teorii únavy materiálu v místě valivého styku. Přesto se nesmí zapomínat, že úplné ložisko lze považovat za soustavu, jejíž každý díl (ložiskové kroužky, valivé elementy, klec, mazivo a těsnění) má stejný vliv na trvanlivost a v některých případech dokonce rozhoduje o skutečné provozní trvanlivosti ložiska. Teoreticky je dosaženo optimální provozní trvanlivosti tehdy, když všechny díly dosáhnou stejné trvanlivosti. Jinými slovy, výpočtová trvanlivost odpovídá skutečné provozní trvanlivosti, jestliže provozní trvanlivost souvisejících dílů je alespoň stejně tak dlouhá jako výpočtová trvanlivost ložiska. Souvisejícími díly jsou v tomto případě klec, těsnění a mazivo. V praxi představuje nejdůležitější faktor únava kovového materiálu.
5.3 Základní dynamická únosnost
Základní dynamická únosnost je podle ISO 281:1990 stálé neproměnné zatížení, které může ložisko teoreticky přenášet při základní trvanlivosti jednoho milionu otáček.Pro radiální ložiska se základní dynamická únosnost Cr vztahuje na stálé neproměnné, čistě radiální zatížení. Pro axiální ložiska se základní axiální dynamická únosnost Ca vztahuje na neproměnné, čistě axiální zatížení, působící v ose ložiska.
Pro každé ložisko je v tabulkové části uvedená základní dynamická únosnost Cr a Ca, jejichž velikost závisí na rozměru ložiska, počtu valivých těles, materiálu a konstrukci ložiska. Hodnoty základních dynamických únosností byly stanoveny v souladu s normou ISO 281. Tyto hodnoty jsou ověřeny na zkušebních zařízeních a potvrzeny provozními výsledky.
Číselné hodnoty uvedené v tomto katalogu platí pro ložiska z chromové oceli, tepelně zpracované na minimální tvrdost 58 HRC a běžné provozní podmínky. U ložisek NEW FORCE se projevují mj. zlepšené vlastnosti materiálu a moderní výrobní postupy. Proto pro stanovení dynamické únosnosti u těchto ložisek je nutné použít opravné součinitele podle ISO 281. Více je o těchto ložiskách v samostatné kapitole 7.7.
5.4 Trvanlivost
Je to počet otáček, které ložisko vydrží, než nastane u některé jeho části únava, projevující se odlupováním materiálu. Vyjadřuje se buď celkovým počtem otáček, nebo provozních hodin, nebo u vozidel délkou ujeté dráhy (počtem ujetých km).
 Obr 5.1 Ilustrační fotografie únavového poškození na oběžné dráze |
 Obr 5.2 Ilustrační fotografie únavového poškození na oběžné dráze |
Příčina značného rozptylu trvanlivosti u větší série stejných ložisek zkoušených za stejných podmínek je především v materiálu. Žádný materiál, ani ložisková ocel, není zcela homogenní a má určitá slabá místa. Je-li slabé místo na oběžné dráze, kde vzniká při valení velké zatížení (napětí), bude trvanlivost ložiska malá. Je-li na méně zatíženém místě, bude trvanlivost vyšší. Špatný materiál má velké množství slabých bodů a je pravděpodobné, že některé z nich leží v místech největšího namáhání. Rozptyl trvanlivosti bude proto u špatného materiálu menší a u prvotřídního materiálu větší.
Na rozptyl trvanlivosti mají podstatný vliv též výrobní tolerance jednotlivých součástí. Tolerance průměrů valivých těles a poloměry oběžných drah značně ovlivňují namáhání valivých ploch. Z výrobních důvodů kolísá v ložisku radiální vůle v určité toleranci, a tím tedy ovlivňuje i rozdělení tlaku na jednotlivá valivá tělesa. Stejným způsobem ovlivňuje rozdělení sil v ložisku roztažení a zmenšení průměru oběžné dráhy v důsledku předepsaných uložení kroužků na hřídeli a v tělese.
Důležitým ukazatelem jakosti ložiska je i dodržení předepsaného složení materiálu, jeho čistota a tepelné zpracování. Velký rozptyl trvanlivosti většího množství stejných valivých ložisek zkoušených za stejných podmínek je jen přirozeným důsledkem působení uvedených jednotlivých vlivů. Současný výzkum ukázal, že i kvalita maziva, jeho čistota a množství mohou značně ovlivnit trvanlivost ložiska. Mazání je zohledněno ve výpočtu modifikované trvanlivosti, viz dále.
Z provedených výsledků zkoušek trvanlivosti i praktických provozních zkušeností je patrné, že stejná ložiska pracující za totožných podmínek, nedosahují stejné trvanlivosti. Proto je nutné si tento pojem trvanlivosti správně definovat.
5.5 Rovnice základní trvanlivosti
Základní trvanlivost ložiska je matematicky definována rovnicí trvanlivosti, která platí pro všechny typy ložisek.L_10=(C/P)^p anebo C/P=(L_10 )^(1/p)
L_10 - základní trvanlivost [10^6⥂ot]
C - základní dynamická únosnost [kN]
(hodnoty Cr a Ca jsou uvedeny v produktové části katalogu)
P - ekvivalentní dynamické zatížení ložiska [kN]
(rovnice pro výpočet Pr a Pa jsou uvedeny v kapitole Ekvivalentní dynamické zatížení a při každé konstrukční skupině ložisek)
p - mocnitel pro kuličková ložiska p=3
Mocnitel pro ložiska s čárovým stykem p=10/3
Základní trvanlivostí ložiska tedy rozumíme trvanlivost, kterou dosáhne nebo překročí 90% ložisek ze souboru stejných ložisek pracujících při stejných provozních podmínkách. Pro tento stupeň spolehlivosti se provádí všechny standardní výpočty trvanlivosti. Střední trvanlivost Ls, to je trvanlivost, které dosáhne 50% ložisek stejného souboru, je asi 5 krát vyšší než základní trvanlivost. Naopak trvanlivost, kterou dosáhne 99% ložisek je asi pětinová ve srovnání se základní trvanlivostí. Vliv stupně spolehlivosti na výpočet trvanlivosti je uveden v kapitole 5.6.
V tabulce 5.1 je uvedena závislost trvanlivosti L10 v milionech otáček na velikosti poměr C/P. V případě, že se frekvence otáček nemění, může se pro výpočet trvanlivosti použít upravená rovnice, která vyjadřuje základní trvanlivost v provozních hodinách:
L_10h=(C/P)^p⋅(10^6)/(60⋅n)
L_10h - základní trvanlivost [h]
n - frekvence otáček [1/min]
Závislost poměru C/P na základní trvanlivosti L10h a na frekvenci otáček je uvedena pro kuličková ložiska v tabulce 5.2 a pro válečková, jehlová, soudečková a kuželíková ložiska v tabulce 5.3.
| Poměr C/P v závislosti na trvanlivosti L10h | |||||||
| Kuličková ložiska | Ložiska s čárovým stykem | ||||||
| Trvanlivost L10 | C/P | Trvanlivost L10 | C/P | Trvanlivost L10 | C/P | Trvanlivost L10 | C/P |
| x 106ot | x 106ot | x 106ot | x 106ot | ||||
| 0,5 | 0,79 | 600 | 8,43 | 0,5 | 0,81 | 600 | 6,81 |
| 0,75 | 0,91 | 650 | 8,66 | 0,75 | 0,92 | 650 | 6,98 |
| 1 | 1,00 | 700 | 8,88 | 1 | 1,00 | 700 | 7,14 |
| 1,5 | 1,14 | 750 | 9,09 | 1,5 | 1,13 | 750 | 7,29 |
| 2 | 1,26 | 800 | 9,28 | 2 | 1,24 | 800 | 7,43 |
| 3 | 1,44 | 850 | 9,47 | 3 | 1,39 | 850 | 7,56 |
| 4 | 1,59 | 900 | 9,65 | 4 | 1,52 | 900 | 7,70 |
| 5 | 1,71 | 950 | 9,83 | 5 | 1,62 | 950 | 7,82 |
| 6 | 1,82 | 1 000 | 10,00 | 6 | 1,71 | 1 000 | 7,94 |
| 8 | 2,00 | 1 100 | 10,30 | 8 | 1,87 | 1 100 | 8,17 |
| 10 | 2,15 | 1 200 | 10,60 | 10 | 2,00 | 1 200 | 8,39 |
| 12 | 2,29 | 1 300 | 10,90 | 12 | 2,11 | 1 300 | 8,59 |
| 14 | 2,41 | 1 400 | 11,20 | 14 | 2,21 | 1 400 | 8,79 |
| 16 | 2,52 | 1 500 | 11,40 | 16 | 2,30 | 1 500 | 8,97 |
| 18 | 2,62 | 1 600 | 11,70 | 18 | 2,38 | 1 600 | 9,15 |
| 20 | 2,71 | 1 700 | 11,90 | 20 | 2,46 | 1 700 | 9,31 |
| 25 | 2,92 | 1 800 | 12,20 | 25 | 2,63 | 1 800 | 9,48 |
| 30 | 3,11 | 1 900 | 12,40 | 30 | 2,77 | 1 900 | 9,63 |
| 35 | 3,27 | 2 000 | 12,60 | 35 | 2,91 | 2 000 | 9,78 |
| 40 | 3,42 | 2 200 | 13,00 | 40 | 3,02 | 2 200 | 10,10 |
| 45 | 3,56 | 2 400 | 13,40 | 45 | 3,13 | 2 400 | 10,30 |
| 50 | 3,68 | 2 600 | 13,80 | 50 | 3,23 | 2 600 | 10,60 |
| 60 | 3,91 | 2 800 | 14,10 | 60 | 3,42 | 2 800 | 10,80 |
| 70 | 4,12 | 3 000 | 14,40 | 70 | 3,58 | 3 000 | 11,00 |
| 80 | 4,31 | 3 500 | 15,20 | 80 | 3,72 | 3 500 | 11,50 |
| 90 | 4,48 | 4 000 | 15,90 | 90 | 3,86 | 4 000 | 12,00 |
| 100 | 4,64 | 4 500 | 16,50 | 100 | 3,98 | 4 500 | 12,50 |
| 120 | 4,93 | 5 000 | 17,10 | 120 | 4,20 | 5 000 | 12,90 |
| 140 | 5,19 | 5 500 | 17,70 | 140 | 4,40 | 5 500 | 13,20 |
| 160 | 5,43 | 6 000 | 18,20 | 160 | 4,58 | 6 000 | 13,60 |
| 180 | 5,65 | 7 000 | 19,10 | 180 | 4,75 | 7 000 | 14,20 |
| 200 | 5,85 | 8 000 | 20,00 | 200 | 4,90 | 8 000 | 14,80 |
| 250 | 6,30 | 9 000 | 20,80 | 250 | 5,24 | 9 000 | 15,40 |
| 300 | 6,69 | 10 000 | 21,50 | 300 | 5,54 | 10 000 | 15,80 |
| 350 | 7,05 | 12 500 | 23,20 | 350 | 5,80 | 12 500 | 16,90 |
| 400 | 7,37 | 15 000 | 24,70 | 400 | 6,03 | 15 000 | 17,90 |
| 450 | 7,66 | 17 500 | 26,00 | 450 | 6,25 | 17 500 | 18,70 |
| 500 | 7,94 | 20 000 | 27,10 | 500 | 6,45 | 20 000 | 19,50 |
| 550 | 8,19 | 25 000 | 29,20 | 550 | 6,64 | 25 000 | 20,90 |
| Poměr C/P v závislosti na trvanlivosti L10h a frekvenci otáček n pro kuličková ložiska | |||||||||||||||||||||||||||||
| Trvanlivost L10h | Frekvence otáčení n [min-1] | ||||||||||||||||||||||||||||
| Hod | 10 | 16 | 25 | 40 | 63 | 100 | 125 | 160 | 200 | 250 | 320 | 400 | 500 | 630 | 800 | 1 000 | 1 250 | 1 600 | 2 000 | 2 500 | 3 200 | 4 000 | 5 000 | 6 300 | 8 000 | 10 000 | 12 500 | 16 000 | |
| 100 | - | - | - | - | - | - | - | - | 1,06 | 1,15 | 1,24 | 1,34 | 1,45 | 1,56 | 1,68 | 1,82 | 1,96 | 2,12 | 2,29 | 2,47 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | |
| 500 | - | - | - | 1,06 | 1,24 | 1,45 | 1,56 | 1,68 | 1,82 | 1,96 | 2,12 | 2,29 | 2,47 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | |
| 1 000 | - | - | 1,15 | 1,34 | 1,56 | 1,82 | 1,96 | 2,12 | 2,29 | 2,47 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | |
| 1 250 | - | 1,06 | 1,24 | 1,45 | 1,68 | 1,96 | 2,12 | 2,29 | 2,47 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | |
| 1 600 | - | 1,15 | 1,34 | 1,56 | 1,82 | 2,12 | 2,29 | 2,47 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | |
| 2 000 | 1,06 | 1,24 | 1,45 | 1,68 | 1,96 | 2,29 | 2,47 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | |
| 2 500 | 1,15 | 1,34 | 1,56 | 1,82 | 2,12 | 2,47 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | |
| 3 200 | 1,24 | 1,45 | 1,68 | 1,96 | 2,29 | 2,67 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | |
| 4 000 | 1,34 | 1,56 | 1,82 | 2,12 | 2,47 | 2,88 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | |
| 5 000 | 1,45 | 1,68 | 1,96 | 2,29 | 2,67 | 3,11 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | |
| 6 300 | 1,56 | 1,82 | 2,12 | 2,47 | 2,88 | 3,36 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | |
| 8 000 | 1,68 | 1,96 | 2,29 | 2,67 | 3,11 | 3,63 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | |
| 10 000 | 1,82 | 2,12 | 2,47 | 2,88 | 3,36 | 3,91 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | |
| 12 500 | 1,96 | 2,29 | 2,67 | 3,11 | 3,36 | 4,23 | 4,56 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | |
| 16 000 | 2,12 | 2,47 | 2,88 | 3,36 | 3,91 | 4,56 | 4,93 | 5,23 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | |
| 20 000 | 2,29 | 2,67 | 3,11 | 3,63 | 4,23 | 4,93 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | |
| 25 000 | 2,47 | 2,88 | 3,36 | 3,91 | 4,56 | 5,32 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | |
| 32 000 | 2,67 | 3,11 | 3,63 | 4,23 | 4,93 | 5,75 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | 31,10 | |
| 40 000 | 2,88 | 3,36 | 3,91 | 4,56 | 5,32 | 6,20 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | 31,10 | - | |
| 50 000 | 3,11 | 3,63 | 4,23 | 4,93 | 5,75 | 6,70 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | 31,10 | - | - | |
| 63 000 | 3,36 | 3,91 | 4,56 | 5,32 | 6,20 | 7,23 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | 31,10 | - | - | - | |
| 80 000 | 3,36 | 4,23 | 4,93 | 5,75 | 6,70 | 7,81 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | 31,10 | - | - | - | - | |
| 100 000 | 3,91 | 4,56 | 5,32 | 6,20 | 7,23 | 8,43 | 9,11 | 9,83 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | 31,10 | - | - | - | - | - | |
| 200 000 | 4,93 | 5,75 | 6,70 | 7,81 | 9,11 | 10,60 | 11,50 | 12,40 | 13,40 | 14,50 | 15,60 | 16,80 | 18,20 | 19,60 | 21,20 | 22,90 | 24,70 | 26,70 | 28,80 | 31,10 | - | - | - | - | - | - | - | - | |
| Poměr C/P v závislosti na trvanlivosti L10h a frekvenci otáček n pro ložiska s čárovým stykem | |||||||||||||||||||||||||||||
| Trvanlivost L10h | Frekvence otáčení n [min-1] | ||||||||||||||||||||||||||||
| Hod | 10 | 16 | 25 | 40 | 63 | 100 | 125 | 160 | 200 | 250 | 320 | 400 | 500 | 630 | 800 | 1 000 | 1 250 | 1 600 | 2 000 | 2 500 | 3 200 | 4 000 | 5 000 | 6 300 | 8 000 | 10 000 | 12 500 | 16 000 | |
| 100 | - | - | - | - | - | - | - | - | 1,05 | 1,10 | 1,21 | 1,30 | 1,39 | 1,49 | 1,60 | 1,71 | 1,83 | 1,97 | 2,11 | 2,26 | 2,42 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | |
| 500 | - | - | - | 1,05 | 1,21 | 1,39 | 1,49 | 1,60 | 1,71 | 1,83 | 1,97 | 2,11 | 2,26 | 2,42 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,70 | 5,54 | 5,94 | 6,36 | |
| 1 000 | - | - | 1,13 | 1,30 | 1,49 | 1,71 | 1,83 | 1,97 | 2,11 | 2,26 | 2,42 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | |
| 1 250 | - | 1,05 | 1,21 | 1,39 | 1,60 | 1,83 | 1,97 | 2,11 | 2,26 | 2,42 | 2,59 | 52,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | |
| 1 600 | - | 1,13 | 1,30 | 1,49 | 1,71 | 1,97 | 2,11 | 2,26 | 2,42 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | |
| 2 000 | 1,05 | 1,21 | 1,39 | 1,60 | 1,83 | 2,11 | 2,26 | 2,42 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | |
| 2 500 | 1,13 | 1,30 | 1,49 | 1,71 | 1,97 | 2,26 | 2,42 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | |
| 3 200 | 1,21 | 1,39 | 1,60 | 1,83 | 2,11 | 2,42 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | |
| 4 000 | 1,30 | 1,49 | 1,71 | 1,97 | 2,26 | 2,59 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | |
| 5 000 | 1,39 | 1,60 | 1,83 | 2,11 | 2,42 | 2,78 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | |
| 6 300 | 1,49 | 1,71 | 1,97 | 2,26 | 2,59 | 2,97 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | |
| 8 000 | 1,60 | 1,83 | 2,11 | 2,42 | 2,78 | 3,19 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | |
| 10 000 | 1,71 | 1,97 | 2,26 | 2,59 | 2,97 | 3,42 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | |
| 12 500 | 1,83 | 2,11 | 2,42 | 2,78 | 3,19 | 3,66 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | |
| 16 000 | 1,97 | 2,26 | 2,59 | 2,97 | 3,42 | 3,92 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | |
| 20 000 | 2,11 | 2,42 | 2,78 | 3,19 | 3,66 | 4,20 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | |
| 25 000 | 2,26 | 2,59 | 2,97 | 3,42 | 3,92 | 4,50 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | |
| 32 000 | 2,42 | 2,78 | 3,19 | 3,66 | 4,20 | 4,82 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | - | |
| 40 000 | 2,59 | 2,97 | 3,42 | 3,92 | 4,50 | 5,17 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | - | - | |
| 50 000 | 2,78 | 3,19 | 3,66 | 4,20 | 4,82 | 5,54 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | - | - | - | |
| 63 000 | 2,97 | 3,42 | 3,92 | 4,50 | 5,17 | 5,94 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | - | - | - | - | |
| 80 000 | 3,19 | 3,66 | 4,20 | 4,82 | 5,54 | 6,36 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | - | - | - | - | - | |
| 100 000 | 3,42 | 3,92 | 4,50 | 5,17 | 5,94 | 6,81 | 7,30 | 7,82 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | - | - | - | - | - | - | |
| 200 000 | 4,20 | 4,82 | 5,54 | 6,36 | 7,30 | 8,38 | 8,98 | 9,62 | 10,30 | 11,00 | 11,80 | 12,70 | 13,60 | 14,60 | 15,60 | 16,70 | 17,90 | 19,20 | 20,60 | - | - | - | - | - | - | - | - | - | |
U uložení náprav silničních a kolejových vozidel se základní trvanlivost může vyjádřit upraveným vztahem v počtu ujetých kilometrů.
L_10km=(C/P)^p⋅(π⋅D)/1000
L_10km - základní trvanlivost [10^6 km]
D - průměr kola [m]
5.5.1 Směrné hodnoty základní trvanlivosti
V případech, když není pro dané uložení předem požadovaná trvanlivost, lze za přiměřené považovat hodnoty uvedené v tabulkách 5.4 a 5.5.
| Směrné hodnoty základní trvanlivosti v provozních hodinách | |
| Druh stroje | Základní trvanlivost L10h |
| přístroje a nářadí zřídka používané | 1 000 |
| elektrické stroje pro domácnost, malé ventilátory | 2 000 až 4 000 |
| stroje pro přerušovaný provoz, ruční nástroje, dílenské jeřáby, hospodářské stroje | 4 000 až 8 000 |
| stroje pro přerušovaný provoz s požadovanou vysokou spolehlivostí, pomocné stroje v elektrárnách, pásové dopravníky, dopravní vozíky, výtahy | 8 000 až 15 000 |
| válcovací stolice | 6 000 až 12 000 |
| stroje pro 8—16hodinový provoz, stacionární elektromotory, ozubené převody, vřetena textilních strojů, stroje na zpracování plastů, tiskařské stroje, jeřáby | 15 000 až 30 000 |
| obráběcí stroje všeobecně | 20 000 až 30 000 |
| stroje pro trvalý provoz: stacionární elektrické stroje, dopravní zařízení, válečková dopravníky, čerpadla, odstředivky, dmychadla, kompresory, tlukadlové mlýny, drtiče, briketovací lisy, důlní výtahy, lanové kotouče | 40 000 až 60 000 |
| stroje pro trvalý provoz s velkou provozní bezpečností: elektrárenské stroje, vodárenské stroje, papírenské stroje, lodní stroje | 100 000 až 200 000 |
| Směrné hodnoty základní trvanlivosti v kilometrech | |
| Druh vozidla | Základní trvanlivost L10km |
| Kolová ložiska silničních vozidel | |
| motocykly | 60 000 |
| osobní automobily | 150 000 až 250 000 |
| nákladní automobily, autobusy | 400 000 až 500 000 |
| Nápravová ložiska kolejových vozidel | |
| nákladní železniční vozy (dle UIC) při trvalém působení maximálního zatížení na nápravu | 800 000 |
| tramvaje | 1 500 000 |
| osobní železniční vozy | 3 000 000 |
| motorové vozy a motorové jednotky | 3 000 000 až 4 000 000 |
| lokomotivy | 3 000 000 až 5 000 000 |
5.6 Rovnice upravené trvanlivosti
Provozní trvanlivost, jak bylo již popsáno, záleží na mnoha faktorech. Výzkumy i provozními výsledky bylo prokázáno, že prodloužení trvanlivosti lze dosáhnout při dokonalém mazání, kdy valivé povrchy zcela odděluje vrstva maziva. Rovněž byla prokázaná vyšší odolnost proti únavovému poškození materiálů vyrobených moderními technologickými postupy. Tento pokrok v technickém vývoji byl zahrnut do normy ISO 281jako výpočet upravené (modifikované) trvanlivosti, který do výpočtu zahrnul součinitele spolehlivosti a1, materiálu a2 a provozních podmínek a3. Další výsledky zkoušek přinesly závěry, že vliv materiálu a provozních podmínek, zvláště mazání, spolu úzce souvisí. To vedlo ke sdružení obou součinitelů do jednoho a23.Upravená trvanlivost je tedy korigovaná základní trvanlivost, přičemž se při výpočtu kromě zatížení zohledňuje vliv materiálu ložiskových součástek, fyzikálně – mechanické vlastnosti maziva a teplotní režim pracovního prostředí ložiska.
L_na=a_1⋅a_23⋅L_10
L_na - upravená trvanlivost pro spolehlivost (100 - n) % a jiné než běžné provozní podmínky [10^6 ot]
a_1 - koeficient spolehlivosti pro jinou než 90 % spolehlivost, viz tabulka 5.6
a_23 - koeficient materiálu, maziva, technologie výroby a provozních podmínek, viz obr. 5.3
L_10 - základní trvanlivost [10^6 ot]
| Hodnoty koeficientu a1 | |||
| Spolehlivost (%) | Ln | a1 | |
| 90 | L10 | 1 | |
| 95 | L5 | 0,64 | |
| 96 | L4 | 0,55 | |
| 97 | L3 | 0,47 | |
| 98 | L2 | 0,37 | |
| 99 | L1 | 0,25 | |
| 99,2 | L0,8 | 0,22 | |
| 99,4 | L0,6 | 0,19 | |
| 99,6 | L0,4 | 0,16 | |
| 99,8 | L0,2 | 0,12 | |
| 99,9 | L0,1 | 0,093 | |
| 99,92 | L0,08 | 0,087 | |
| 99,94 | L0,06 | 0,08 | |
| 99,95 | L0,05 | 0,077 | |
Pro základní stanovení hodnot koeficientu a_23 se vychází z diagramu na obr. 5.4.
Kvalita mazacího procesu je dána mírou oddělení valivých ploch. Rozhodujícím faktorem pro tvorbu mazacího filmu je viskozita, která silně závisí na teplotě. O použití maziva rozhoduje viskózní poměr:
κ=υ/υ_1
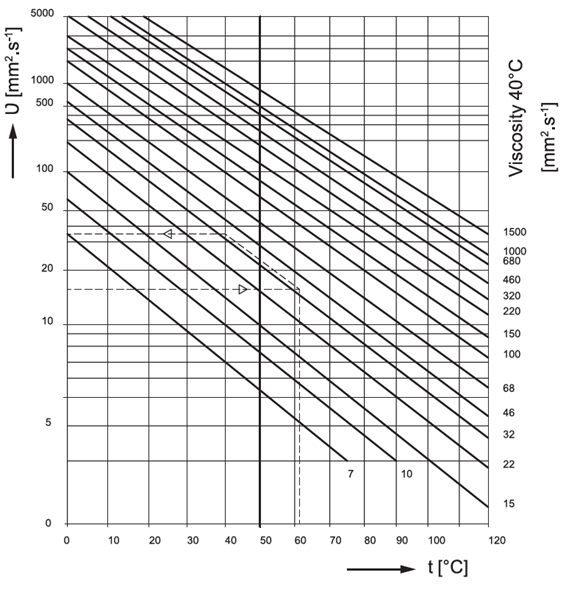
υ - kinematická viskozita maziva při provozní teplotě ložiska [mm^2⋅s^(-1) ]
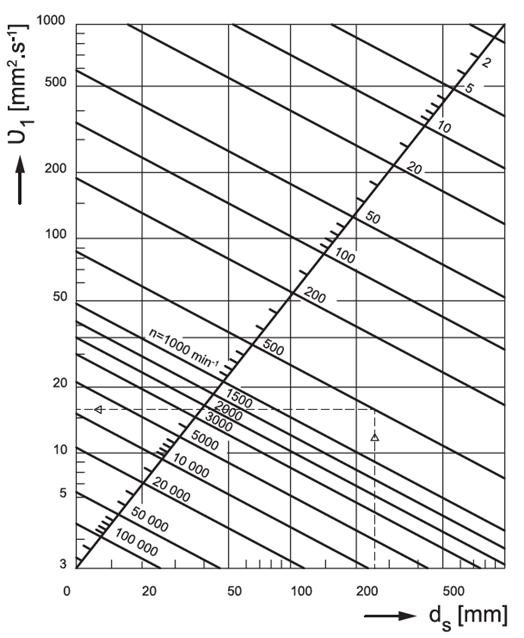
υ_1 - kinematická viskozita pro definovanou frekvenci otáček a zvolený rozměr
ložiska [mm^2⋅s^(-1) ]
Hodnoty υa υ_1 určíme podle diagramu na obrázku 5.4 a 5.5. V diagramu na obr. 5.3, čára I platí pro radiální kuličková ložiska, která pracují ve velmi čistém prostředí. V ostatních případech se koeficient a_23 volí nižší v závislosti na čistotě prostředí, přičemž klesající tendence je závislá na konstrukční skupině ložiska v tomto pořadí:
- Kuličková ložiska s kosoúhlým stykem
- Kuželíková ložiska
- Válečková ložiska
- Dvouřadá naklápěcí ložiska
- Soudečková ložiska
Tuto problematiku doporučujeme konzultovat s technicko-konzultačních služeb ZKL.

Obr. 5.3
Obr. 5.4
Obr. 5.5
5.7 Trvanlivost podle ZKL
Po mnoho let se použití výpočtu základní trvanlivosti L_10 jako kritéria výkonového parametru ložiska ukázalo jako uspokojivé. Tento výpočet je spojen s 90% spolehlivostí, s běžně používanými vysoce kvalitními materiály, kvalitním technologickým provedením a s běžnými provozními podmínkami.Nicméně pro mnoho aplikací se stalo žádoucí výpočet provádět pro jinou úroveň spolehlivosti nebo pro přesnější podmínky mazání a kontaminace. S využitím moderních vysoce kvalitních ložiskových ocelí bylo zjištěno, že za příznivých provozních podmínek a za nižších kontaktních napětí než je jisté limitní a pokud mezní únavové napětí ložiskové oceli není překročeno, je možné dosáhnout vyšších trvanlivostí než je trvanlivost L_10. Na druhou stranu se může stát za nepříznivých provozních podmínek, že trvanlivost ložiska bude kratší než je L_10.
Systémový přístup únavové trvanlivosti byl využit při tvorbě metodiky výpočtu modifikované trvanlivosti dle ZKL. Vliv na trvanlivost systému (ložiska) je popsán v následujícím textu a uvažuje vliv rozptylu a interakce vzájemně propojených faktorů na celkovou životnost.Tyto faktory se projevují zvýšeným kontaktním napětím v kontaktní oblasti a to vede k poklesu životnosti.
Tyto faktory jsou využity v rovnici modifikované trvanlivosti.
L_m=a_1⋅a_ZKL⋅L_10
a_1 - koeficient spolehlivosti pro jinou než 90 % spolehlivost, viz tabulka 5.6
a_ZKL - koeficient modifikované životnosti
L_10 - základní trvanlivost [10^6 ot]
Pokud jsou mazací podmínky, čistota prostředí a ostatní provozní podmínky příznivé, může pod jistým zatížením moderní vysoce kvalitní ložisko dosahovat nekonečné životnosti. Pro ložisko vyrobené z obecně vysoce kvalitního ložiskového materiálu a dobré výrobní kvality je mezní únavové zatížení takové zatížení, které v ložisku vyvodí kontaktní tlak na valivých elementech o velikosti přibližně 1500 MPa. Tato hodnota napětí bere v úvahu přídavná napětí způsobená výrobními tolerancemi a provozními podmínkami. Snížená přesnost výrobku a kvalita materiálu má za následek nižší mezní únavové zatížení.
V mnoha aplikacích jsou kontaktní napětí vyšší než 1500 MPa. Za takových provozních podmínek dochází k snížení životnosti.
Je možné vztáhnout provozní vlivy k aplikovanému napětí a na pevnost materiálu.
- Vruby mají za následek vznik hranových napětí
- Tenký olejový film zvyšuje napětí v kontaktní oblasti mezi oběžnou dráhou a valivým elementem
- Zvýšená teplota snižuje mezní únavové zatížení materiálu (jeho pevnost)
- Pevné uložení vnitřního kroužku (zvětšený přesah) vyvolá zvýšené obvodové napětí
Teoretické vysvětlení o tom, jak zahrnout další vlivy jako je provozní radiální vůle a proměnné napětí na oběžných drahách od vyklopení, je vysvětleno v ISO/TS 16281.
5.7.1 Mezní únavové zatížení
5.7.2 Stanovení koeficientu modifikované trvanlivosti
- Únavové zatížení a zatížení ložiska
- Mazání (typ maziva, viskozitu, rychlost otáček, velikost ložiska, přísady)
- Prostředí (úroveň kontaminace, těsnění)
- Kontaminující částice (tvrdost a velikost částic ve vztahu k velikosti ložiska, metoda mazání, filtrace)
- Montáž (čistota během montáže)
Koeficient únavové trvanlivosti a_ZKL je odvozen z následující rovnice:
a_ZKL=f((e_C⋅C_or)/P,κ)
Faktory e_C a κ berou v úvahu kontaminaci a podmínky mazání.
5.7.3 Faktor znečištění
Snížení životnosti ložiska způsobená vlivem pevných částic v mazivovém filmu závisí:
- Typu, velikosti, tvrdosti a množství částic
- Tloušťce mazivového filmu (relativní viskozitě κ)
- Velikosti ložiska
| Stupeň znečištění | eC | |
| Dpw < 100 mm | Dpw ≥ 100 mm | |
| Extrémní čistota | 1 | 1 |
| Velikost částic v řádu tloušťky mazacího filmu, laboratorní podmínky | ||
| Vysoká čistota | 0,8 až 0,6 | 0,9 až 0,8 |
| Olej filtrovaný přes extrémně jemný filtr, typické podmínky pro ložisko s plastovým krytem a s celoživotní mazivovou náplní | ||
| Normální čistota | 0,6 až 0,5 | 0,8 až 0,6 |
| Olej filtrovaný přes jemný filtr, podmínky typické pro ložisko s plechovým krytem a s celoživotní mazivovou náplní | ||
| Mírné znečištění | 0,5 až 0,3 | 0,6 až 0,4 |
| Mírné znečištění v mazivu | ||
| Typické znečištění | 0,3 až 0,1 | 0,4 až 0,2 |
| Typické podmínky ložisek bez integrovaných těsnění, částice způsobující otěr vstupují do ložiska z okolí | ||
| Silné znečištění | 0,1 až 0 | 0,1 až 0 |
| Prostředí ložiska je silně znečištěno, ložisková uložení s nedostatečným těsněním | ||
| Velmi silné znečištění | 0 | 0 |
Podrobný výpočet faktoru znečištění
V tabulce 5.7 jsou uvedeny přibližné hodnoty faktoru znečištění. Pokud by situace vyžadovala použití přesnějšího výpočtu, je nutné použít přesnější výpočet, který je uveden níže.Faktor znečištění může být stanoven pro následující druhy mazání
- Oběhové olejové mazání s on-line filtrací
- Mazání v olejové lázni nebo oběhové mazání s off-line filtrací
- Mazání plastickým mazivem
β_x=n_1/n_2 , kde
β_x filtrační poměr pro částice stanovené velikosti x
n_1 počet částic na jednotku objemu (100 ml) větších než x, před průchodem filtrem
n_2 počet částic na jednotku objemu (100 ml) větších než x, po průchodu filtrem
Filtrační poměr určuje účinnost filtrů.
Oběhové mazání s on-line filtrací
Filtrační poměr β_x s velikostí částic x v µm podle normy ISO 16889 je nejvíce ovlivňující faktor při výběru příslušného diagramu.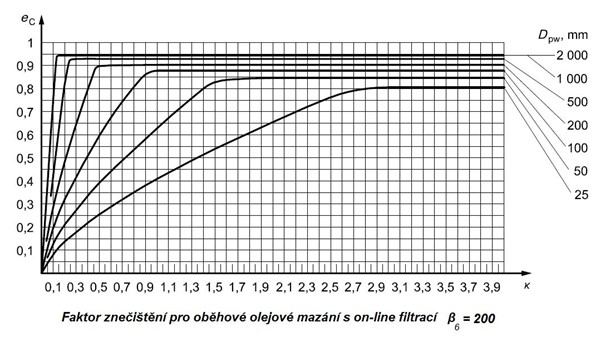
Obr. 5.7
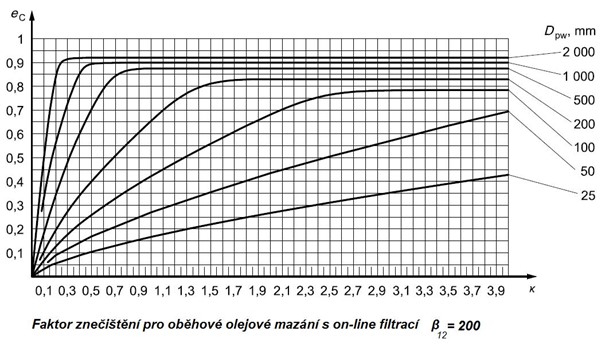
Obr. 5.8
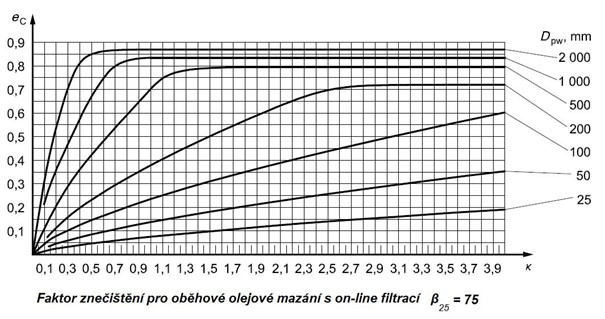
Obr. 5.9
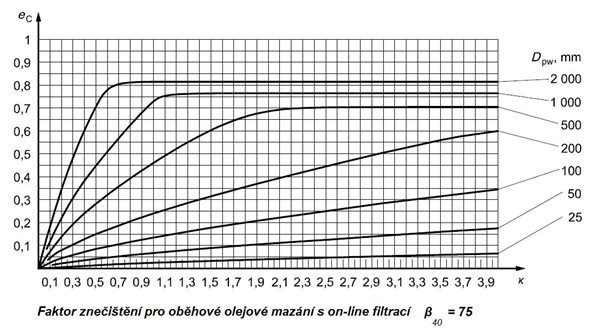
Obr. 5.10
Mazání v olejové lázni nebo oběhové mazání s off-line filtrací
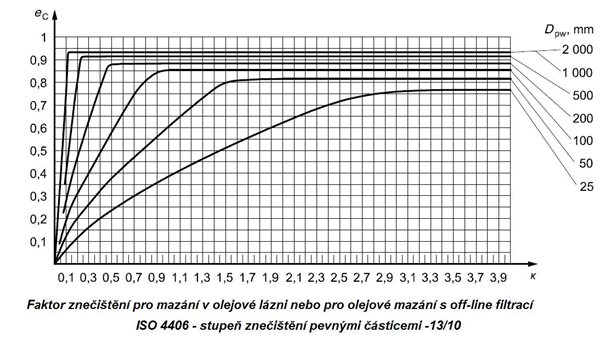
Obr. 5.11
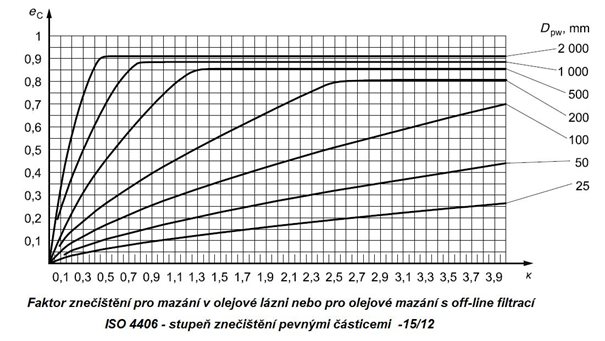
Obr. 5.12
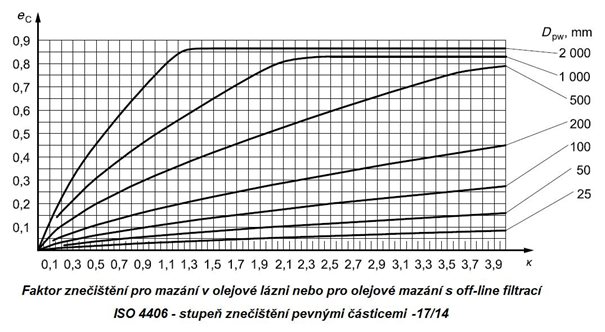
Obr. 5.13
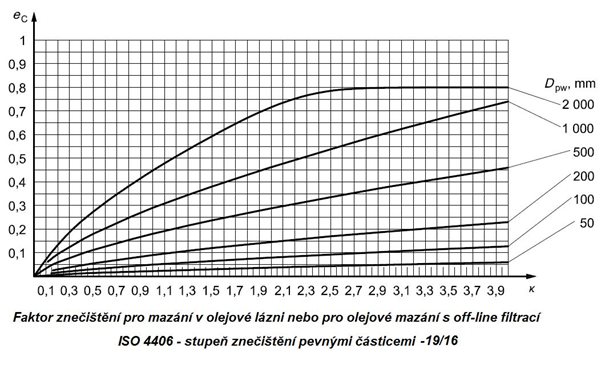
Obr. 5.14
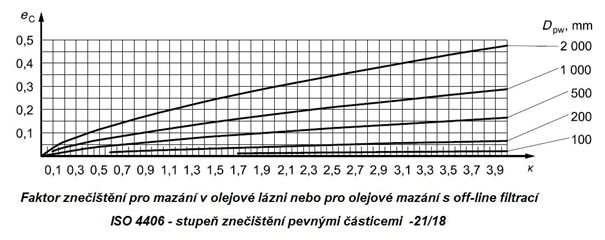
Obr. 5.15
Mazání plastickým mazivem
| Provozní podmínky | Stupeň znečištění |
| Velmi čistá montáž, velmi dobré těsnění ve vztahu k provozním podmínkám, domazávání probíhají kontinuálně nebo v krátkých časových intervalech. (Ložiska s integrovaným těsněním) | Vysoká čistota |
| Čistá montáž, dobré těsnění, domazávání dle specifikace výrobce. (ložiska s integrovaným těsněním) | Obvyklá čistota |
| Čistá montáž, střední těsnící kapacita vzhledem k provozním podmínkám | Mírně znečištění |
| Montáž v dílně, ložisko a uložení není dostatečně vyprané po montáži, špatná těsnící kapacita vzhledem k provozním podmínkám, domazávací intervaly jsou delší než jsou doporučené | Silné znečištění |
| Montáž v znečištěném prostředí, nedostatečné těsnění, dlouhé domazávací intervaly | Velmi silné znečištění |
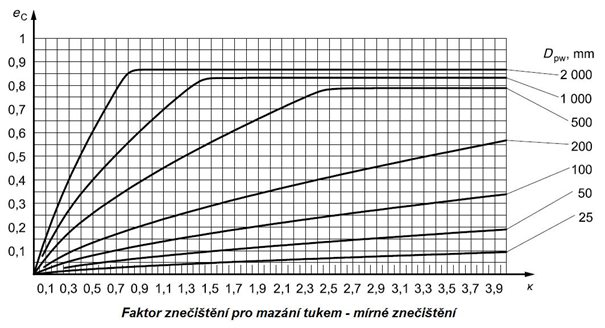
Obr. 5.16
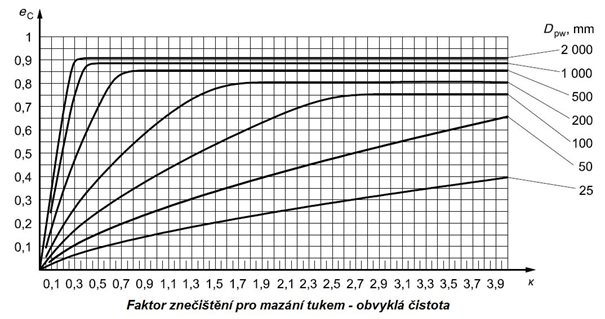
Obr. 5.17
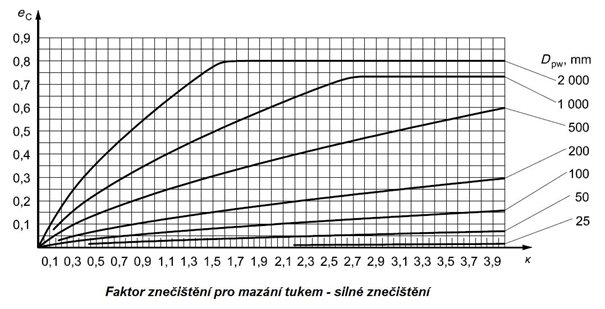
Obr. 5.18
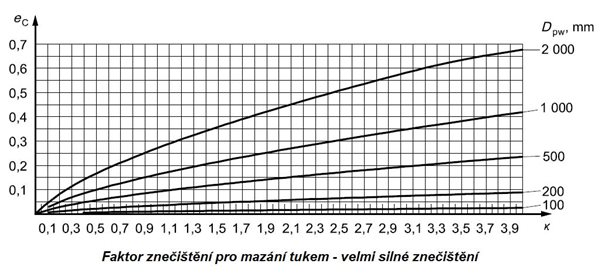
Obr. 5.19
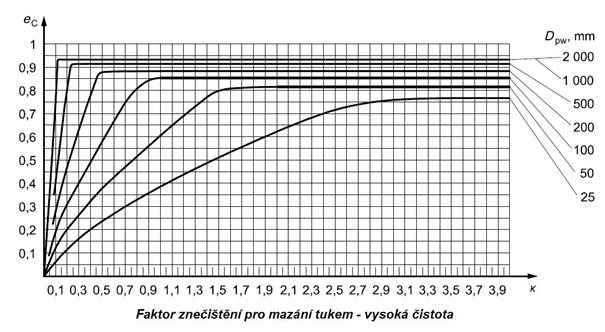
Obr. 5.20
5.7.4 Viskózní poměr
κ=ν/ν_1
Za účelem vytvoření odpovídajícího mazacího filmu si musí mazivo zachovat určitou minimální viskozitu při provozní teplotě. Životnost ložisek může být prodloužena pomocí zvýšení provozní viskozity ν.
Referenční kinematická viskozita může být určena z obrázku č. 5.4 nebo pomocí následujících rovnic
ν_1=45000⋅n^(-0,83)⋅D_pw^(-0,5) for n< 1000 ot/min
ν_1=45000⋅n^(-0,5)⋅D_pw^(-0,5) for n≥ 1000 ot/min
Kde D_pw=0,5⋅(d+D) je střední průměr ložiska
5.7.5 Výpočet koeficientu modifikované trvanlivosti
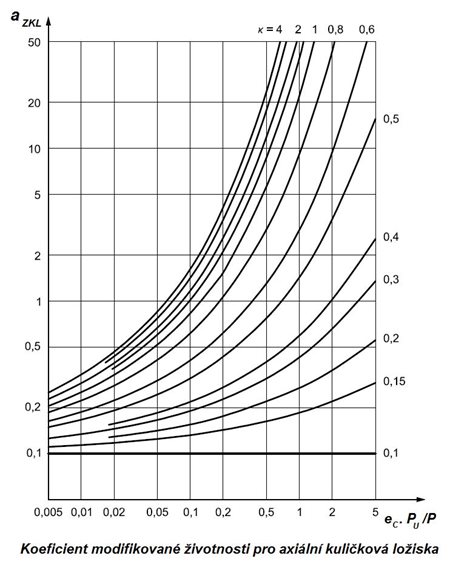
Obr. 5.21
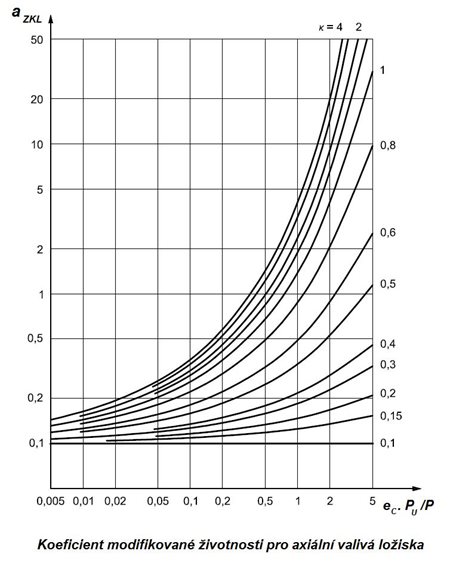
Obr. 5.22
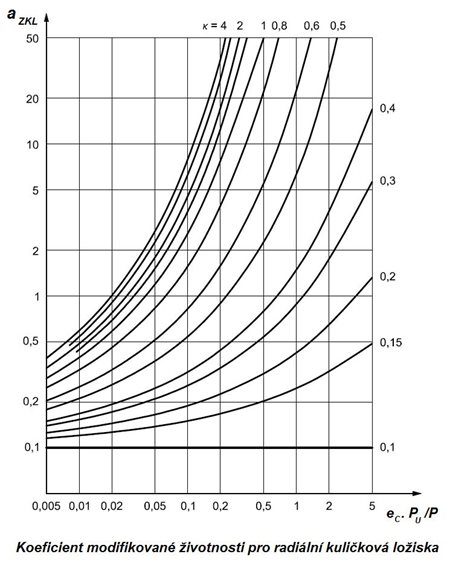
Obr. 5.23
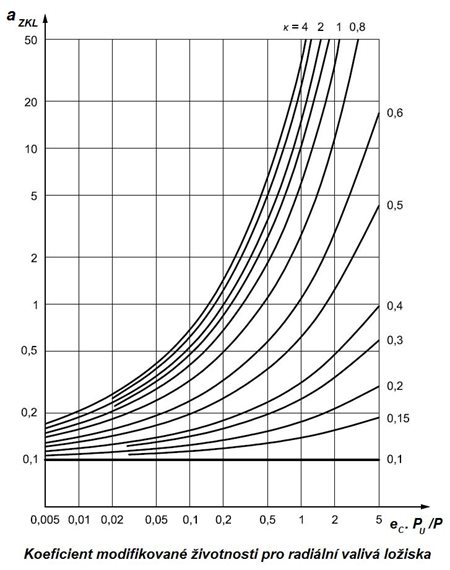
Obr. 5.24
5.8 Ekvivalentní dynamické zatížení
V konstrukčním uzlu je ložisko vystaveno všeobecně působícím silám různé velikosti, při různé frekvenci otáček a s různou dobou působení. Z hlediska metodiky výpočtu je potřebné přepočítat působící síly na konstantní zatížení, při kterém bude mít ložisko stejnou trvanlivost, jakou dosáhne v podmínkách skutečného zatížení. Toto přepočítané konstantní radiální nebo axiální zatížení nazýváme ekvivalentní zatížení P resp. Pr (radiální) nebo Pa (axiální).5.8.1 Kombinované zatížení
Způsob zatížení konstantní
Vnější síly působící na ložisko se nemění ani co do velikosti ani v závislosti na čase.Radiální ložiska
Pokud současně působí na radiální ložisko konstantní síly v radiálním i axiálním směru, platí pro výpočet radiálního ekvivalentního dynamického zatížení rovnice:P_r=X⋅F_r+Y⋅F_a [kN]
P_r - radiální ekvivalentní dynamické zatížení [kN]
F_r - radiální síla působící na ložisko [kN]
F_a - axiální síla působící na ložisko [kN]
X - koeficient radiálního zatížení
Y - koeficient axiálního zatížení
Koeficienty X a Y jsou závislé na poměru Fa / Fr. Hodnoty X a Y jsou uvedeny v tabulkové části nebo v komentáři před každou konstrukční skupinou, kde jsou uvedeny bližší údaje pro výpočet ložisek příslušné konstrukční skupiny.
Axiální ložiska
Axiální kuličková ložiska mohou přenášet jen síly působící v axiálním směru a pro výpočet ekvivalentního axiálního dynamického zatížení platí rovnice:P_a=F_a [kN]
P_a - axiální ekvivalentní dynamické zatížení [kN]
F_a - axiální zatížení ložiska [kN]
Axiální soudečková ložiska mohou přenášet i určitá radiální zatížení, avšak jen při současném působení axiálního zatížení, přičemž musí být splněna podmínka
P_a=F_a+1,2⋅F_r [kN]
Způsob zatížení proměnný
Skutečné proměnné zatížení, jehož časový průběh je znám, se pro výpočet nahrazuje středním myšleným zatížením. Toto myšlené zatížení má na ložisko stejný vliv jako skutečné proměnné zatížení.5.8.2 Změna velikosti zatížení při stálé frekvenci otáček
F_s=(∑_(i=1)^n▒〖〖F_i〗^3⋅q_i/100〗)^(1/3) [kN]
F_s - myšlené střední neproměnné zatížení [kN]
F_i=F_1,...,F_n - neproměnné dílčí skutečné zatížení [kN]
q_i=q_1,...,q_n - podíl působení dílčích zatížení [%]
Jestliže působí na ložisko v čase proměnlivé zatížení a přitom se mění i frekvence otáčení (obr. 5.26), vypočítá se střední myšlené zatížení z rovnice
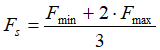 [kN]
[kN]
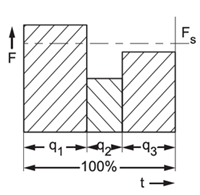 Obr. 5.25 |
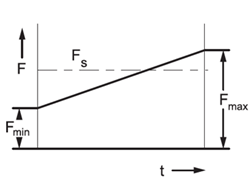 Obr. 5.26 |
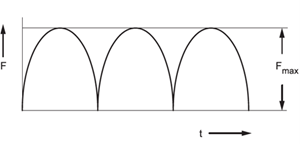 Obr. 5.27 |
 Obr. 5.28 |
Pokud má skutečné zatížení sinusový průběh (obr. 5.27), je střední myšlené zatížení
F_s=0,75⋅F_max [kN]
5.8.3 Změna velikosti zatížení při změně frekvence otáček
F_s=((∑_(i=1)^n▒〖F_i^3⋅q_i⋅n_i 〗)/(∑_(i=1)^n▒〖q_i⋅n_i 〗))^(1/3) [kN]
n_i=n_1,...,n_n - konstantní frekvence otáček během působení dílčích zatížení F_1,...,F_n [〖min〗^(-1)]
q_i=q_1,...,q_n podíl působení dílčích zatížení a frekvencí [%]
Pokud se v závislosti na čase mění jen frekvence otáček, myšlená střední frekvence otáček se vypočítá z rovnice
n_s=(∑_(i=1)^n▒g_i ⋅n_i)/100 [〖min〗^(-1)]
n_s - střední frekvence otáček [〖min〗^(-1)]
5.8.4 Kývavý pohyb ložiska
F_s=F_r⋅(γ/90)^(1/p) [kN]
F_s - střední myšlené zatížení [kN]
F_r - skutečné radiální zatížení [kN]
γ - amplituda kývavého pohybu [°]
p - mocnitel pro kuličková ložiska p=3
Pro válečková, jehlová, soudečková a kuželíková ložiskap=10/3
5.9. Vliv teploty
Dodávaný sortiment ložisek je určený pro použití v prostředí s teplotou do 120°C. Soudečková a ložiska větších rozměrů jsou standardně vyráběna pro provoz do 200°C. Výjimku tvoří některá dvouřadá soudečková ložiska s polyamidovými vodícími kroužky a jednořadá kuličková ložiska s těsněním (RS, 2RS, RSR, 2RSR), která jsou použitelná krátkodobě do teploty 150°C. Blíže o těchto ložiskách v kapitole 12 Údaje o výrobcích.Pro vyšší provozní teploty jsou valivá ložiska vyrobena tak, aby byly zabezpečeny jejich potřebné fyzikálně – mechanické vlastnosti a rozměrová stabilita. Řešení uložení při vyšších provozních teplotách doporučujeme konzultovat s dodavatelem.
Hodnoty základní dynamické únosnosti Cr nebo Ca uváděné v tabulkové části publikace, je potřebné v případě vyšších provozních teplot násobit koeficientem ft, který je uveden v tabulce 5.9.
| Hodnoty koeficientu ft | ||||
| provozní teplota do [ ° ] | 150 | 200 | 250 | 300 |
| koeficient ft | 0,95 | 0,9 | 0,75 | 0,6 |
5.10 Základní statická únosnost
Radiální základní statická únosnost Cor a axiální základní statická únosnost Coa je pro každé ložisko uvedena v tabulkové části publikace. Hodnoty Cor a Coa byly stanoveny výpočtem podle mezinárodní normy ISO 76.Základní statická únosnost je zatížení, které odpovídá vypočítaným stykovým napětím v nejvíc zatíženém pásmu styku valivého tělesa a oběžné dráhy ložiska:
- 4600 MPa pro dvouřadá naklápěcí kuličková ložiska
- 4200 MPa pro ostatní kuličková ložiska
- 4000 MPa pro ložiska s čárovým stykem
Statická únosnost ložiska Cor se používá pro výpočet, jestliže ložiska
- se otáčejí s velmi nízkou rychlostí otáčení (n < 10 min-1)
- provádějí velmi pomalé oscilační pohyby
- se pod zatížením nepohybují určitou delší dobu.
Maximální zatížení, které může působit na ložisko, by mělo být použito ve výpočtu ekvivalentního statického zatížení ložiska.
5.10.1 Ekvivalentní statické zatížení
P_or=X_o⋅F_r+Y_o⋅F_a [kN]
P_oa=Y_o⋅F_a [kN]
P_or - radiální ekvivalentní statické zatížení [kN]
P_oa - axiální ekvivalentní statické zatížení [kN]
F_r - radiální zatížení [kN]
F_a - axiální zatížení [kN]
X_o - koeficient radiálního zatížení
Y_o - koeficient axiálního zatížení
| Koeficient statické bezpečnosti s0 | |||
| Pohyb ložiska | Způsob zatížení, požadavky na chod ložiska | s0 | |
| Kuličková ložiska | Ložiska s čárovým stykem | ||
| otáčivý | "výrazné nárazové zatížení, vysoké požadavky na klidný chod" |
2 | 4 |
| po statickém zatížení se ložisko otáčí při nižším zatížení | 1,5 | 3 | |
| normální požadavky na klidný chod | |||
| normální provozní podmínky a normální požadavky na chod | 1 | 1,5 | |
| klidný chod bez otřesů | 0,5 | 1 | |
| kývavý | malý úhel výkyvu s velkou frekvencí s nárazovým nerovnoměrným zatížením | 2 | 3,5 |
| velký úhel výkyvu s malou frekvencí s přibližně stálým periodickým zatížením | 1,5 | 2,5 | |
| neotáčivý (v klidu) | výrazné nárazové zatížení | 1,5 až 1 | 3 až 2 |
| normální a malé zatížení, na chod ložiska nejsou kladeny zvláštní nároky | 1 až 0,4 | 2 až 0,8 | |
| axiální soudečková ložiska při všech druzích pohybu a zatížení | - | 4 | |
Koeficienty X0 a Y0 jsou uvedeny v tabulkové části publikace. Zároveň jsou tu uvedeny bližší údaje pro stanovení ekvivalentního statického zatížení ložisek dané konstrukční skupiny.
5.10.2 Bezpečnost ložisek při statickém zatížení
V praxi se bezpečnost ložisek při statickém zatížení zjišťuje z poměru Cor/Por nebo Coa/Poa a porovnává se s údaji v tabulce 5.10, kde jsou uvedeny hodnoty nejmenších přípustných koeficientů s0 pro různé provozní podmínky.
s_0=C_or/P_or anebo C_oa/P_oa
s_0 - koeficient bezpečnosti při statickém zatížení [kN]
C_or - radiální základní dynamická únosnost [kN]
C_oa - axiální základní dynamická únosnost [kN]
P_or - radiální ekvivalentní statické zatížení resp. při výrazném nárazovém zatížení max. působící síla Frmax (obr. 5.29) [kN]
P_oa - axiální ekvivalentní statické zatížení resp. při výrazném nárazovém zatížení max. působící síla Frmax (obr. 5.29) [kN]
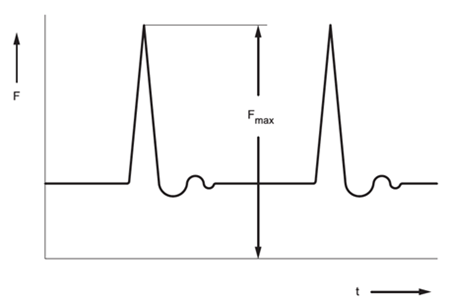
Obr. 5.29
